MySQL深入:B+树的演化和操作

1. 二叉查找树

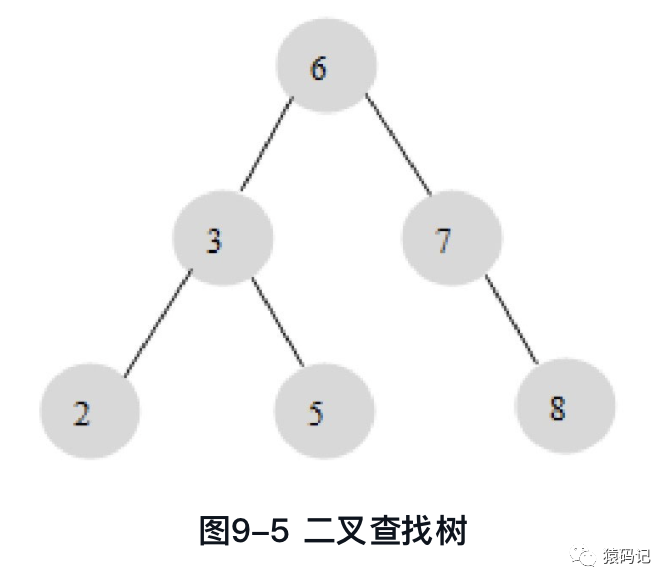
在二叉查找树中，左子树的键值总是小于根的键值，右子树的键值总是大于根的键值，因此可以通过中序遍历得到键值的排序输出。对上图进行中序遍历(左-根-右)后输出：2、3、5、6、7、8

对图9-5的这棵二叉树进行查找，如查找键值为5的记录，先找到根，其键值是6，6大于5，因此查找6的左子树，找到3；而5大于3，再找右子树……一共找了3次。如果按2、3、5、6、7、8的顺序来找同样需要3次。用同样的方法再查找键值为8的这条记录，这次用了3次查找，而顺序查找时需要6次。如果计算平均查找次数可得：顺序查找的平均查找次数为（1+2+3+4+5+6）/6=3.3次，二叉查找树的平均查找次数为（3+3+3+2+2+1）/6=2.3次。二叉查找树比顺序查找的平均效率要高。

2. 平衡二叉树(AVL)

2.1 由来

二叉查找树可以任意构造，同样是2、3、5、6、7、8这五个数字，也可以按照图9-6的方式建立二叉查找树

图9-6的平均查找次数为（1+2+3+4+5+5）/6=3.16次，和顺序查找差不多。显然这棵二叉查找树的效率就差很多。因此若想最大性能地构造一个二叉查找树，需要这棵二叉查找树是平衡的，因此引入了新的定义—平衡二叉树，又称为AVL树，平衡二叉树的定义如下：首先符合二叉查找树的定义，其次必须满足任何节点的两棵子树的高度最大差为1。

平衡二叉树在查找方面的性能是比较高的，但不是最高的，只是接近最高性能。要达到最好的性能需要建立一棵最优二叉树，但是最优二叉树的建立和维护需要大量的操作，因此一般只需建立一棵平衡二叉树即可。

2.2 缺点

平衡二叉树的查询速度的确很快，但是维护一棵平衡二叉树的代价非常大，通常需要1次或多次左旋或右旋来得到经过插入或更新操作后二叉树的平衡性。

一次旋转操作:

对于图9-5所示的平衡树，当我们需要插入一个新的键值为9的节点时，需要做如图9-7所示的变动:

这里通过一次左旋操作就将插入后的树重新变为平衡二叉树。但是有的情况可能需要进行多次的旋转操作，如图9-8所示。

**总结: **对一棵平衡树的维护是有一定开销的，不过平衡二叉树多用于内存结构对象中，因此维护的开销相对较小。

3.B+树

3.1 介绍

• 由来： B+树由B树和索引顺序访问方法演化而来，但是在实现过程中几乎没有使用B树的情况了。
• 概念： B+树是为磁盘或其他直接存取辅助设备设计的一种平衡查找树，在B+树中，所有记录节点都是按键值的大小顺序存放在同一层的叶子节点，各叶子节点通过指针进行链接
• 

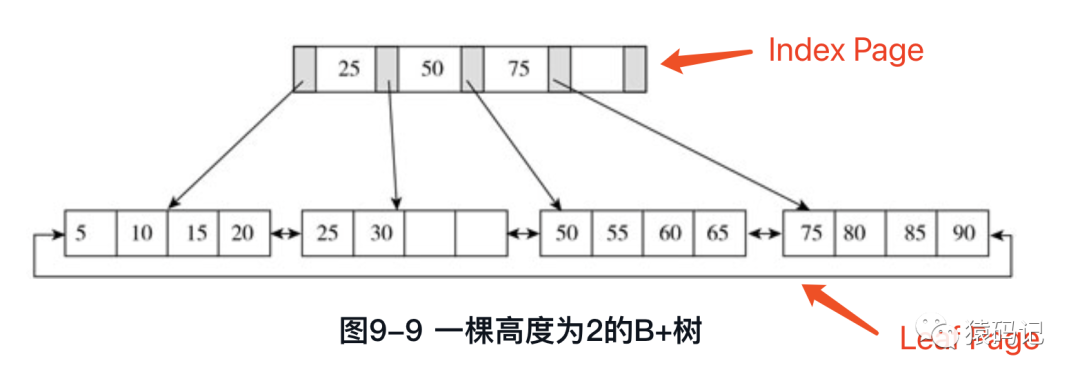
4.B+树操作

4.1 插入

B+树的插入要求必须保证插入后叶子节点中的记录依然顺序排列，同时需要考虑插入到B+树的3种情况，每种情况都可能导致不同的插入算法，如表9-1所示:

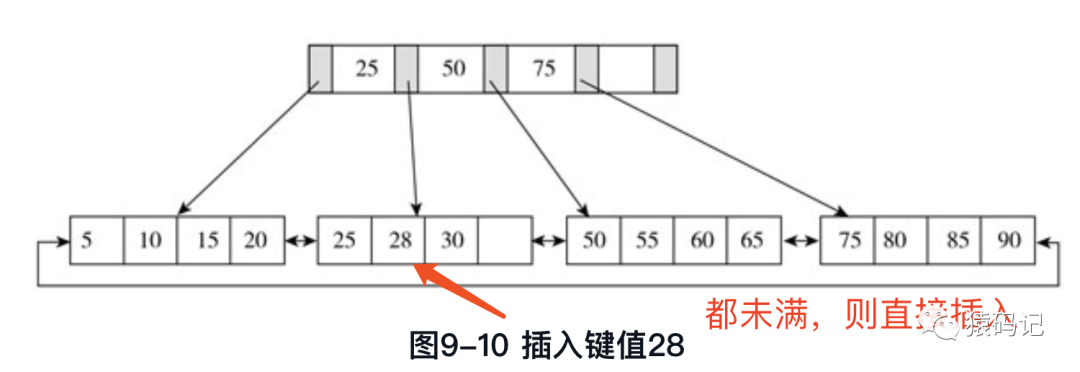
a. 情况一:都未满

对于图9-9中的这棵B+树，我们插入28这个键值，发现当前Leaf Page和Index Page 都没有满，直接插入就可以了，如图9-10所示。

b. 情况二:Leaf Page 已满

继续操作再插入70这个键值，这时原先的Leaf Page
已经满了，但是Index Page 还没有满，符合表9-1的第二种情况，将70插入Leaf Page 后的情况为50、55、60、65、70。我们根据中间值60拆分叶子节点，可得图9-11

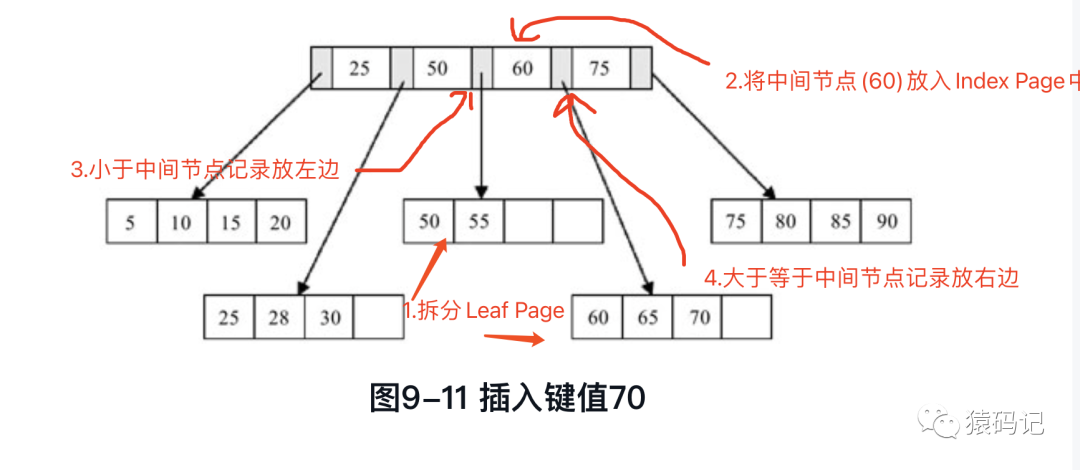
@注意: 由于版面的关系，这次没有能在各叶子节点间标上双向链表指针。不过和图9-9、图9-10一样，这个指针还是存在的

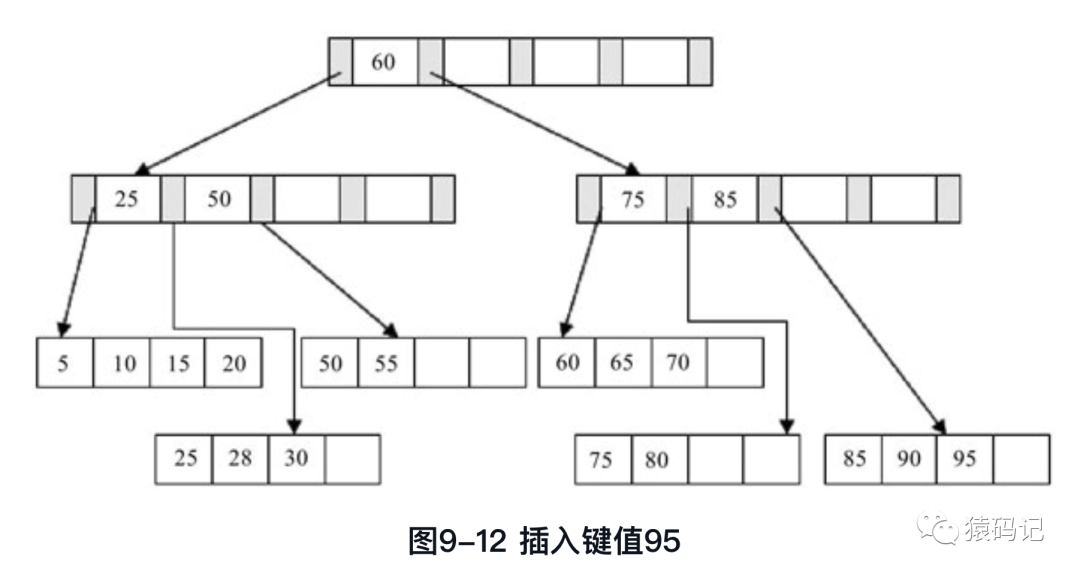
c. 情况三:都满

最后插入记录95，这符合表9-1讨论的第三种情况，即Leaf Page 和Index Page 都满了，这时需要做两次拆分，如图9-12所示。

4.2 旋转

可以看到，不管怎么变化，B+树总会保持平衡，但是为了保持平衡需要在插入新的键值后做大量的拆分页（split）操作，而B+树主要用于磁盘，因此页的拆分意味着磁盘的操作，应该在可能的情况下减少页的拆分。为此，B+树提供了旋转（rotation）的功能。

旋转发生在Leaf Page
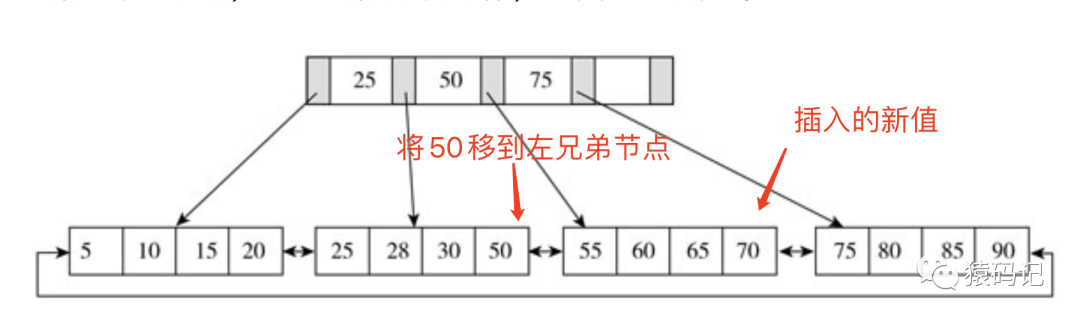
已经满而其左右兄弟节点没有满的情况下。这时B+树并不会急于进行拆分页的操作，而是将记录移到所在页的兄弟节点上。通常先判断左兄弟是否被用来做旋转操作。

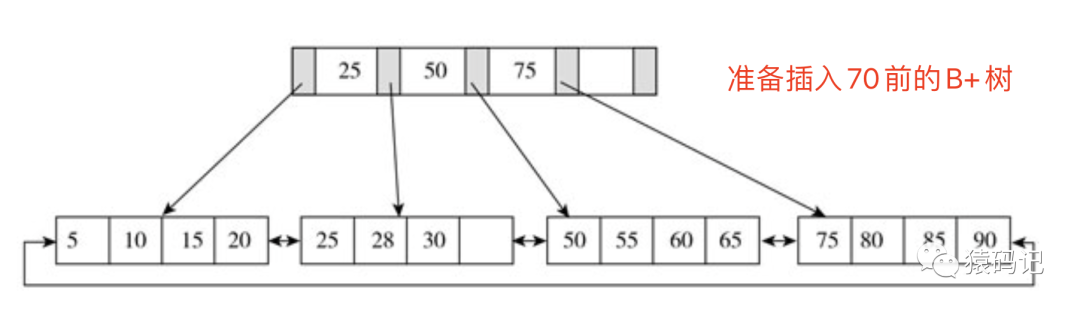
对下图准备进行插入70的操作，此时B+树并不会急于拆分叶子节点，而是去做旋转操作。

执行旋转前:

执行旋转后:

4.3 删除

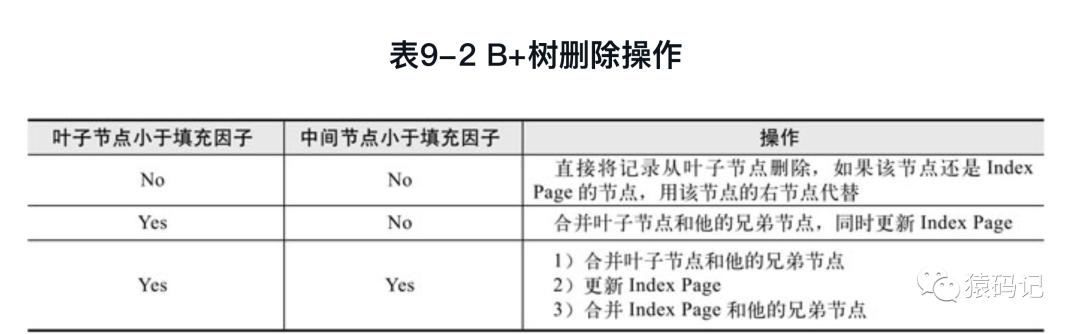
B+树使用填充因子（fill factor）来控制树的删除变化，填充因子可设的最小值是50%。B+树的删除操作同样必须保证删除后叶子节点中的记录依然按序排列。同插入一样， B+树的删除操作同样需要考虑以下3种情况。与插入不同的是，删除根据填充因子的变化来衡量。

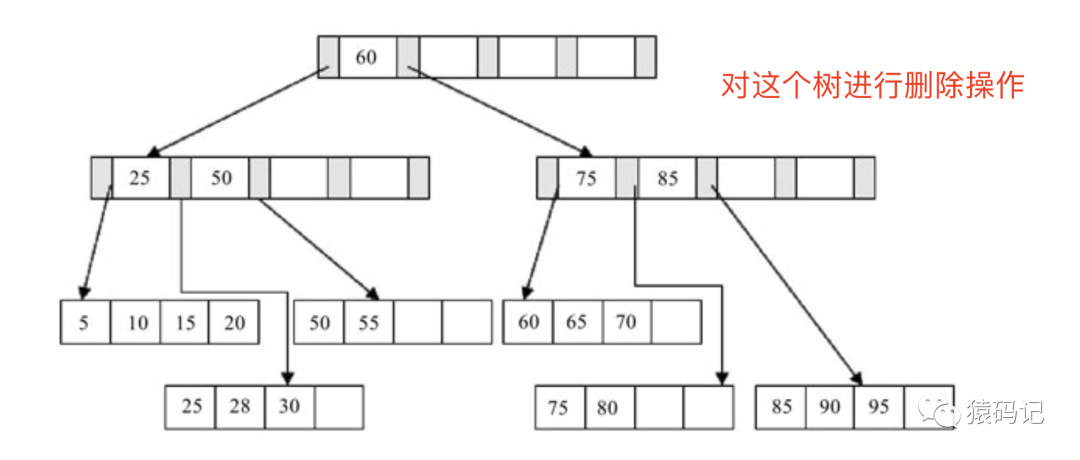
a. 属情况一且不是Index Page节点

首先删除键值为70的这条记录，这符合表9-2讨论的第一种情况，删除后可得图9-14所示的B+树

b. 属情况一且是Index Page 节点

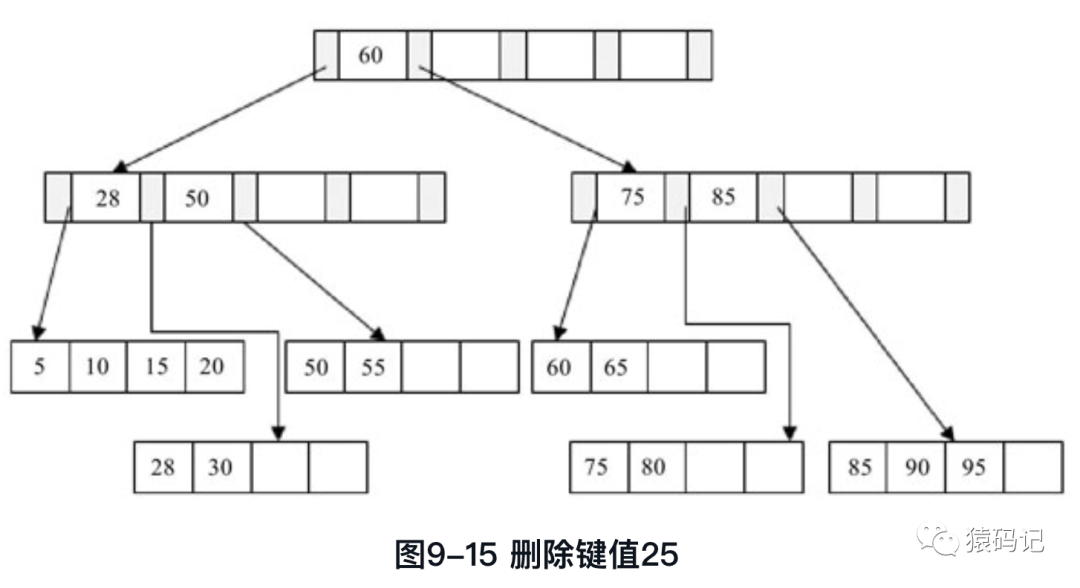
接着删除键值为25的记录，这也符合表9-2讨论的第一种情况，但是该值还是Index Page 中的值，因此在删除Leaf Page中的25后，还应将25的右兄弟节点28更新到Page Index中，最后可得图9-15

c. 属情况二和三

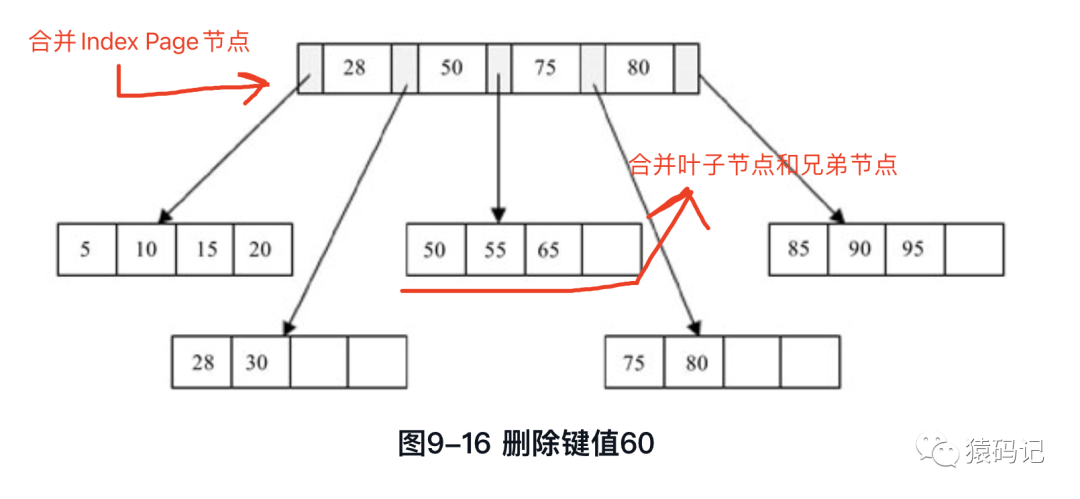
最后来看删除键值60的情况。删除Leaf Page中键值为60的记录后，填充因子小于50%，这时需要做合并操作，同样，在删除Index Page中相关记录后需要做IndexPage的合并操作，最后得图9-16